Introduction
Scale-free networks are a global pattern approach in complex networks, unlike localized approaches such as Causality network analysis or Neural Net. The former aims to identify confounding factors, while the latter focuses on the relationship between edge weight and nodes.
The term "scale" refers to mean value of the degree of node distribution. This means the degree of nodes that are typically obtained stably when selecting a node randomly. This represents the scale of the network. For instance, if the value of $k$ is 7 in a random network, then 7 is considered the scale of the network.
Degree Distribution
The degree distribution is a fundamental characteristic of scale-free networks. In a scale-free network, the degree distribution follows a power law, which means that the probability of a node having $k$ connections is proportional to $k^{-γ}$, where $γ$ is a constant exponent. This means that a few nodes have many connections while most nodes have only a few connections.
Mathematically, the degree distribution can be written as:
$$P(k) ∝ k^{-γ}$$
where $P(k)$ is the probability of a node having $k$ connections and $γ$ is the exponent that characterizes the degree distribution.
Random network vs. Scale free network
- Random network
- Degree distribution: Poisson

- Scale free network
- Degree distribution: Power Law

💡 Using $2^{nd}$ moment, we can show that the variance of Power Law diverges
https://jaehong-data.tistory.com/27
정리
Network에서 scale이란, node를 무작위로 선택했을때 일반적으로 안정적으로 얻어지는 node의 degree (node에 edge가 몇개가 연결되어있는가를 나타내는) 를 의미한다. 때문에 scale free란 무작위로 선택했을때 안정적으로 나오는 값이 없는 그래프를 의미하며, 재미있게도 이는 node 가 많이 연결된 hub node가 조금 존재하고, 대부분의 node는 아주 조금만 연결되는 구조를 갖춘 그래프의 양상을 보인다.
이를 수치적으로 파악하기 위해서는 node별 degree의 분포를 보면되는데, 일반적으로 무작위 연결성을 보이는 random network는 Poisson distribution (이 분포를 기준으로 scale을 예상가능) 을 보이고, scale-free network에서는 Power law disrtibution을 보인다. 아래 그림 참고.


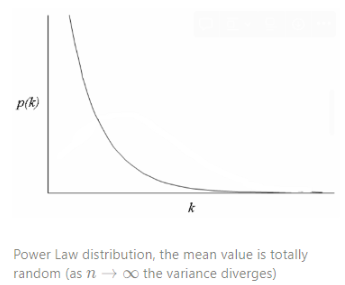

그렇다면 과연 정말 node degree의 분포가 Power law를 따를 때에, 그래프의 node를 임의로 선택했을 때, 안정적으로 나오는 degree 값이 없는것일까? 이는 Power law distribution의 variance가 발산한다는 것을 보이면 된다. 손으로 발산하는것을 증명한 포스트를 예전에 어디선가 (기억이 안남 ㅠㅠ) 발견하여 직접 확인했고, 아래의 포스트에 적어놓았다.
https://jaehong-data.tistory.com/27
그 이외에도 과연 그래프가 "scale free" 한지 보기위한 regression 접근방법, WGCNA에 정리해놓았다. 그래프의 node degree에 대해 log-log transformation 한뒤 regression의 R제곱 값 (결정계수) 이 큰 그래프가 scale free에 가까운 네트워크라 보면 된다는 아이디어다. 실제로, Random network보다 Scale free network가 조금 더 큰 결정계수를 갖는다. 약간의 detail은 나중에 포스팅하면, WGCNA/Power term 부분을 확인 바란다. 아래는 Poisson과 Power law를 결정계수의 관점에서 간단히 비교한 example code를 작성한 것이다.
Reference
Wikipedia
'정리 조금 > Basics' 카테고리의 다른 글
| SSH, Host Keys (0) | 2023.10.12 |
|---|---|
| Expectation vs. Average (0) | 2023.09.04 |
| Exact & Asymptotic p-values (0) | 2023.08.31 |
| Replicates (0) | 2023.08.28 |
| F1 score (0) | 2023.01.13 |